With the ultimate goal of finding the optimal protocols (values of the controls over time) to the ground state of a many-body Hamiltonian, we classicaly simulate this for small feasible system sizes. For larger system sizes where classical simulation isn't feasible, the use of a quantum device is a promising alternative. This would involve starting with some easy-to-prepare initial state, and making a guess for the evolution which evolves the initial state into the desired ground state. Finding the desired ground state requires minimizing the measured energy of the post-evolution state. At a plateau, evolution is likely evolving into the target ground state. However, the complexity of the parameter space makes finding the optimal path to this ground state difficult. Our work aims to mitigate this by finding patterns in the paths for classically feasible system sizes, which can then be extrapolated to inform efficient optimization on the chip. We introduce many new metrics for the protocols and succesfully find patterns across system sizes, along with creating and introducing state-of-the-art algorithms that find these optimal protocls.
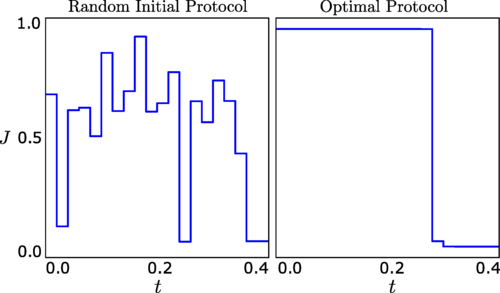
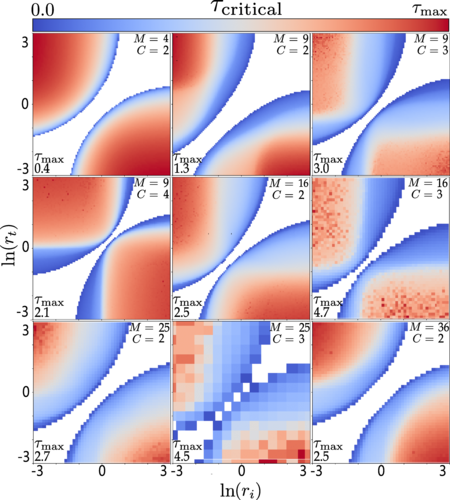
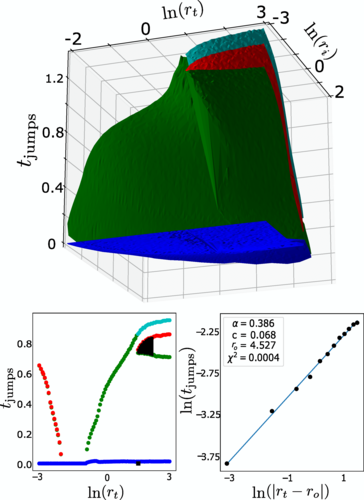
Abstract: In this work, we address the challenge of uncovering patterns in variational optimal protocols for taking the system to ground states of many-body Hamiltonians, using variational quantum algorithms. We develop highly optimized classical Monte Carlo (MC) algorithms to find the optimal protocols for transformations between the ground states of the square-lattice XXZ model for finite systems sizes. The MC method obtains optimal bang-bang protocols, as predicted by Pontryagin's minimum principle. We identify the minimum time needed for reaching an acceptable error for different system sizes as a function of the initial and target states and uncover correlations between the total time and the wave-function overlap. We determine a dynamical phase diagram for the optimal protocols, with different phases characterized by a topological number, namely the number of on-pulses. Bifurcation transitions as a function of initial and final states, associated with new jumps in the optimal protocols, demarcate these different phases. The number of pulses correlates with the total evolution time. In addition to identifying the topological characteristic above, i.e., the number of pulses, we introduce a correlation function to characterize bang-bang protocols' quantitative geometric similarities. We find that protocols within one phase are indeed geometrically correlated. Identifying and extrapolating patterns in these protocols may inform efficient large-scale simulations on quantum devices.